How can we compress and transfer knowledge from a bigger model or ensemble of models(which were trained on very large datasets to extract structure from data) to a single small model without much dip in performance?

But why do we want to do this? Why we need a smaller model when a bigger model or ensemble model is already giving great results on test data?

At training time we typically train large/ensemble of models because the main goal is to extract structure from very large datasets. We could also be applying many things like dropout, data augmentation at train times to feed these large models all kinds of data.

But at prediction time our objective is totally different. We want to get results as quickly as possible. So using a bigger/ensemble of models is very expensive and will hinder deployment to large number of users. So, now the question is how can we compress knowledge from this bigger model into a smaller model which can be easily deployed.

Geoffrey Hinton, Oriol Vinyals, and Jeff Dean from google through their paper came up with a different kind of training called distillation to transfer this knowledge to the smaller model. This is the same technique which hugging face used in their Distill BERT implementation.

If we can train this smaller model to generalize in the same way as a large model, then this smaller model trained this way will do much better than the smaller model trained on the same data but in the normal way. This is one of the main principles behind Distillation

Dark Knowledge:

Usually, in Machine learning, a model that learns to discriminate between a large number of classes, the main training objective is to maximize the average log probability of correct answer. For example, take the example of the MNIST dataset where the goal is to classify an image as to whether it’s 1 or 2 or … 9. So if the actual image is 2 then the objective of any model is to maximize P(its 2/image) (which can be read as probability that a particular image is 2 given the image). But the model also gives probabilities to all incorrect answers even though those probabilities are very small, some of them are much larger than others. Point is that even though these probabilities are small, relative probabilities of incorrect answers tell us a lot about how the model can generalize. To understand it, let’s have a look at the below example

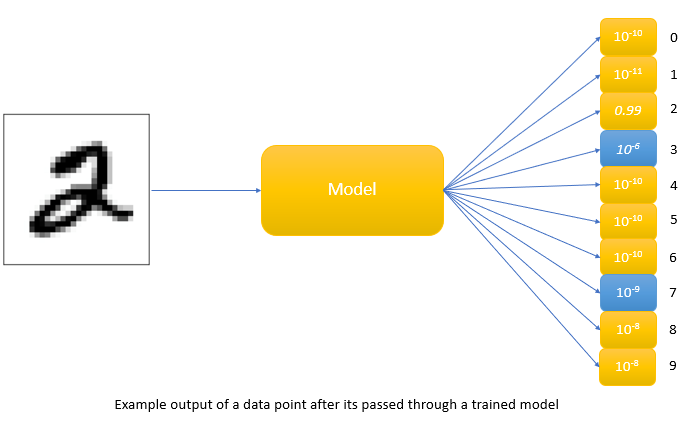
In the above figure, this version of 2 was given a probability of 10^-6 of being a 3 and 10^-9 of being a 7 whereas for another version it may be the other way around. This is valuable information that defines a rich similarity structure over the data(i. e. it says which 2’s look like 3’s and which look like 7’s) but it has very little influence on the cross-entropy cost function during the transfer stage because the probabilities are so close to zero.

But before we move on to the distillation procedure, let’s spend time on how the model actually produced output probabilities. This is where softmax activation comes in. Last step of model processing is softmax and this component is what gives output probabilities. Input to softmax is called logits and we design the final layer of NN in such a way that number of hidden units = number of classes we want to classify.

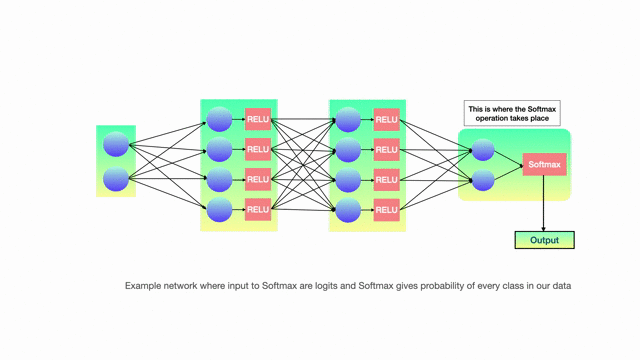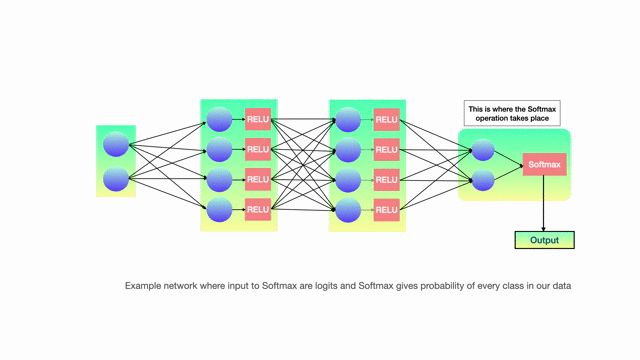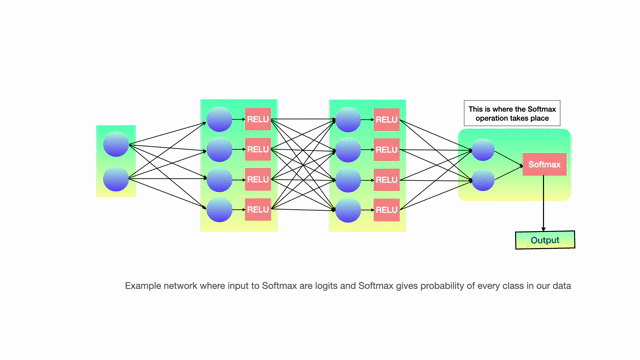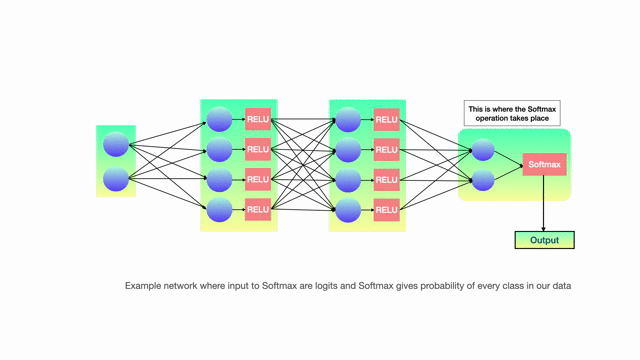
The formula for calculating softmax is given as

The above equation gives probabilities for each i and the sum of all probabilities overall i equals 1. During training time, loss for any single training example is calculated by comparing these softmax probabilities with hard targets(labels) and using backpropagation coefficients are updated until the loss is minimum.

As seen above this softmax gives a high probability to a true label and low probabilities to incorrect labels. We also see that probabilities of incorrect answers even though small, have lot of information hidden in them which helps the model to generalize. We call this Dark Knowledge

Distillation procedure:

According to the paper, the best way to transfer generalization capabilities of the larger model to a small model is to use class probabilities produced by the cumbersome model as soft targets for training the small model.

So the process is as follows:

• Take the original training set which was used to train the bigger model then pass that training data through the bigger model and get softmax probabilities over different classes. As seen above true label will get high probability and incorrect labels will get low probabilities. But we saw these low probabilities have a lot of information hiding in them. So to magnify importance of these probabilities authors of the papers used a variable called Temperature(T) to divide all logits before passing through softmax. This produces a softer probability distribution over classes. We can see below

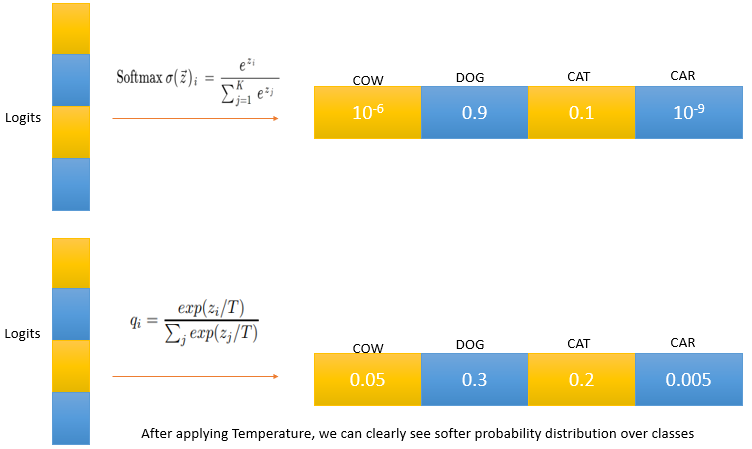
The output of applying softmax with temperature(T) is what we call Soft targets. This process is what authors called distillation. Analogy with removing impurities in water by increasing temperature

• Much of information about learned function from large model resides in the ratios of very small probabilities in the soft targets.

• Some terminology:

  Soft targets - output from the large model after temperature T has been applied during softmax

  Soft predictions - output from the smaller model after temperature T has been applied during softmax

  Hard predictions - output from smaller model when temperature T = 1(regular softmax)

  True targets - actual targets from training set

Below is a flowchart of the entire training process

So training process for a small model has 2 loss functions. The first loss function takes both soft predictions and soft targets and is the cross-entropy loss function. This is the way generalization ability is transferred from large model to small model by trying to match soft targets. For this loss function, both softmax uses the temperature of ‘T’

Authors also found that using the small model to match true targets helps. This is incorporated in the second cost function. The final cost is a weighted average of these two cost functions with hyperparameters alpha and beta.

Experiment on MNIST

The authors used the MNIST dataset to test this approach. They used two architectures for this which differs only in the number of hidden units in middle layers. The authors used 2 hidden layer neural network in both cases

1) Smaller model which can be viewed as 784 -> 800 -> 800 -> 10 (where 784 is unrolled dimensions of an image, 800 is the number of hidden units with RELU activation and 10 is the number of classes we are predicting). This model gave 146 test errors with no regularization.

2) Bigger model which can be viewed as 784 -> 1200 -> 1200 -> 10 (where 784 is unrolled dimensions of an image, 1200 is the number of hidden units with RELU activation and 10 is the number of classes we are predicting). This model is trained on MNIST using dropout, weight-constraints, and jittering input images and this net achieved 67 test errors.

Can we transfer this improvement in the bigger model to a small model?

Authors now used both soft targets obtained from the big net and true targets without dropout and no jittering of images i.e, the smaller net was regularized solely by adding the additional task of matching soft targets produced by the large net at a temperature of 20 and the result is

74 test erros using 784 -> 800 -> 800 -> 10

This shows that soft targets can transfer a great deal of knowledge to the small model, including the knowledge about how to generalize that is learned from translated training data. In other words, the benefit we got from transforming inputs transfers across to the little net even though we are not transforming inputs for the small net.

It’s well-known fact that transforming inputs by different transformations make the model generalize much better and in our case information about how to generalize is showing up in Dark knowledge and this is hiding in soft targets. None of this information is in True targets. So by using information from soft targets our small net is performing much better.

Big net using soft targets learned similarity metric that learned ‘what’s like what’ and with this knowledge transfer, we are telling the little net ‘what’s like what’

All of above experiment on MNIST is summarized below

Additional experiment on MNIST

In addition, authors also tried omitting examples of digit 3 when training a smaller model using distillation. So from the perspective of the small model, 3 is a mythical digit that it has never seen. Since the smaller model has never seen 3 during training, we expect it to make a lot of errors when encountering 3 in the test set. Despite this, the distilled model only made 206 test errors of which 133 are on 1010 threes in the test set. This clearly shows that generalization capabilities of the large model were transferred to the small model during distillation and this causes the small model to correctly predict 3 in most cases

So moral of the story is.

Transforming input images greatly improves generalization. Transforming the targets also has a similarly large effect and if we can get soft targets from somewhere it’s much cheaper as we can get the same performance with the smaller model

References:

1) Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. “Distilling the knowledge in a neural network.”

2) Knowledge distillation by intellabs.